The Nyquist stability criterion is a criterion for judging the stability of a closed-loop system based on the open-loop frequency response of a closed-loop control system, proposed by American scholar H. Nyquist in 1932. The frequency response determined by the control system after the feedback is turned off is called the open loop frequency response. The Nyquist stability criterion is essentially a graphical analysis method, and the open-loop frequency response is easily determined by calculation or experimental means, so it is very convenient and intuitive to apply. The Nyquist stability criterion can only be used in linear stationary systems.
In classical control theory, the Nyquist stability criterion is mainly used to analyze the stability of a univariate system. The frequency response method formed on this basis is one of the main analysis and synthesis methods of classical control theory. Since the 1970s, the Nyquist stability criterion has been extended to multivariate systems (see multivariate frequency domain methods).
First conclusion, Nyquist stability criterion:
If the Nyquist curve does not pass through the (-1, j0) point, and the system is stable when Z = P - 2N = 0, if the Nyquist curve crosses the (-1, j0) point, the system is critically stable.
Where Z is the number of zeros surrounding the function
P is the number of poles of the open-loop transfer function
N is the number of turns surrounded by the Nyquist curve (-1, j0)
It looks very abstract. At the beginning, I remembered the theorem and went to the exam. To understand the Nyquist stability criterion, we must talk about the Cauchy theorem in the complex variable function, which is the argument of the argument. The principle of the argument is actually a circle of circles. It is not detailed here. Please refer to the "complex function" by yourself.
According to the argument of the argument, when s moves clockwise on the closed trajectory without passing through the pole, the value of F(s) moves clockwise on the complex plane ZP week (and the book may be different, but this is very Good understanding).
In fact, the change of the s variable along the closed trajectory corresponds to the F(s) value corresponding to the change in the complex plane.
Why emphasize clockwise? And look at me slowly, hehe!
The closed-loop transfer pole is actually equivalent to the zero of F(s)=1+G(s)H(s), then the stability decision is reduced to the fact that the zero of the F(s) is determined in the right half of the complex plane. Distribution.
The motion trajectory of F(s) on the complex plane can be obtained by shifting the motion trajectory of G(s)H(s) to the right by 1 unit length;
To study the zero distribution of F(s), we must first find a suitable s variable motion trajectory. The book uses two parts:
Semicircle with infinite radius in the right half plane
Virtual axis itself
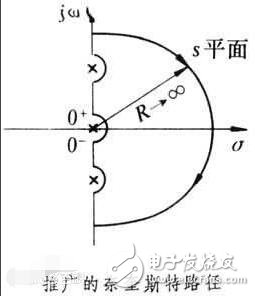
Exception: If there is an open-loop pole at the origin, it is avoided by an arc with an infinite radius, forming a closed curve similar to a sector.
If we choose the trajectory of the s variable to be symmetric about the real axis, we can see from the nature of the complex operation that the motion trajectory of G(s)H(s) is symmetric about the real axis, that is, the motion trajectory of F(s) is symmetric about the real axis.
In this case, we only need to study: the relationship between the trajectory of the corresponding s variable in the upper half of the imaginary axis and the G(s)H(s) trajectory is good, which is why the textbook has R = 2 * N. The number of the lower part is directly multiplied by 2.
So we analyze only the s variable trajectory in the red part of the above figure corresponds to the number of turns of (-1, 0j) around the motion trajectory of G(s)H(s). Then, according to the Nyquist curve and the possible complement lines, the motion "track" of the G(s)H(s) corresponding to the motion trajectory of the upper half plane of the s variable can be obtained. Another part of the symmetry of the trajectory corresponds to the lower half of the s motion trajectory, which is the blue part of the above figure. Corresponding to this word, it is actually a mapping.
The imaginary axis part corresponds to jw, and at the same time, the s variable movement direction is clockwise, then the corresponding w changes from 0 to infinity, so the red part of the imaginary axis corresponds to the N(N) of G(s)H(s). Curve
And the ring portion corresponding to the red infinite radius converges to 0 or a constant when the number of open-loop transfer points is greater than or equal to zero.
If the open-loop letter has a zero point of achievement, then there will be an arc with an infinite radius at the origin. As shown in the above picture, of course, it is not too small, for the sake of good looks.
This arc corresponds to the G(s)H(s) motion trajectory is the complement of the infinite radius (of course, not necessarily a circle, just for the convenience of imagination)
Then you can get the value of Z - P, here also pay attention to the direction of the Nyquist curve. Clockwise or counterclockwise, it affects the sign. I am lazy, I don’t specify it, leave it to you. The reader wants it.
Speaking of this is almost the same, the value of ZP obtained by Nyquist and the possible complement, can be derived from the value of P (the number of poles of open-loop transfer) (F(s)=1 + G(s) The number of zeros of H(s), that is, the number of poles of the closed-loop transmission) Z
DADNCELL alkaline zinc-manganese dry battery has the characteristics of low self-discharge, which is suitable for household batch procurement storage, and has the discharge performance of continuous discharge time with more long-lasting and large instantaneous discharge. Widely used in flashlights, smart door locks, infrared thermometers, cameras, flash lights, razors, electric toys, instruments, high-power remote control, Bluetooth wireless mouse keyboards and other common household electronic equipment instruments. DADNCELL battery advocates providing a more comfortable and smooth power supply experience for household appliances. The alkaline battery capacity and discharge time of the same model of DADNCELL battery have reached four to seven times that of ordinary batteries, respectively.
The performance difference between the two is greater at high and low temperatures, because its unique internal components are structure and battery materials with better performance, and the power capacity and electrical performance can be improved.
At present, all types of batteries developed by DADNCELL Lab do not involve any heavy metals in production, use and waste. They are green and environmentally friendly and can be treated with domestic waste.
1.5V Am-1 Alkaline Cells,All-Purpose Alkaline Batteries,Premium Alkaline D Cell Batteries,Batteries Camera Meters
Shandong Huachuang Times Optoelectronics Technology Co., Ltd. , https://www.dadncell.com